10506. Компоненты
связности список смежности
Найдите количество компонент
связности в графе, заданном списком смежности.
Вход.
В первой строке содержится количество вершин n (1 ≤ n ≤ 10000). Далее идут n строк. В i-ой
строке содержится описание всех рёбер, исходящих из i-ой вершины. Описание начинается
количеством исходящих рёбер. Далее следуют номера вершин, в которые эти рёбра
идут. Все вершины нумеруются натуральными числами от 1 до n.
Выход.
Выведите количество компонент связности.
|
Пример входа |
Пример выхода |
|
6 2 5 6 0 0 1 5 2 1 4 1 1 |
3 |
РЕШЕНИЕ
графы
Анализ алгоритма
Построим список смежности
графа. При помощи поиска в глубину найдем количество компонент связности.
Пример
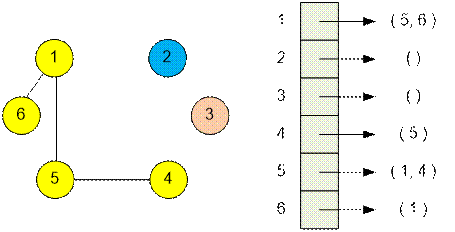
Граф содержит
три компоненты связности.
Реализация алгоритма
Объявим список смежности графа g и массив used.
vector<vector<int>> g;
vector<int> used;
Функция dfs реализует поиск в глубину из вершины v.
void dfs(int v)
{
used[v] = 1;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (!used[to]) dfs(to);
}
}
Основная часть программы. Читаем входные данные. Строим
список смежности.
scanf("%d", &n);
g.resize(n + 1);
used.resize(n + 1);
for (i = 1;
i <= n; i++)
{
scanf("%d", &k);
for (j = 0; j < k; j++)
{
scanf("%d", &x);
g[i].push_back(x);
}
}
Запускаем поиск в глубину. В переменной cnt подсчитываем
количество компонент связности.
cnt = 0;
for (i = 1;
i <= n; i++)
if (used[i] == 0)
{
dfs(i);
cnt++;
}
Выводим ответ.
printf("%d\n", cnt);
Реализация алгоритма – union – find
#include <cstdio>
#include <vector>
using namespace std;
vector<vector<int>> g;
vector<int> used, mas;
int i, j, n, x, k, cnt;
int Repr(int n)
{
while (n != mas[n]) n = mas[n];
return n;
}
void Union(int x, int y)
{
int x1 = Repr(x), y1 = Repr(y);
if (x1 == y1) return;
mas[x1] = y1;
}
int main(void)
{
scanf("%d", &n);
g.resize(n + 1);
mas.resize(n + 1);
for (i = 1; i <=
n; i++)
{
scanf("%d", &k);
for (j = 0; j <
k; j++)
{
scanf("%d", &x);
g[i].push_back(x);
}
}
for (i = 1; i <=
n; i++) mas[i] = i;
for (i = 1; i <=
n; i++)
{
for (j = 0; j <
g[i].size(); j++)
{
int to = g[i][j];
Union(i, to);
}
}
cnt = 0;
for (i = 1; i <=
n; i++)
if (mas[i] == i) cnt++;
printf("%d\n", cnt);
return 0;
}